Introduction

Hi, this is MynaWallet’s zkp grant phase3 report. This phase3 report is the end of the Grant that the MynaWallet team received from Ethereum Foundation in August 2023.

In this report, we will summarize the implementation of the zk circuit that selectively discloses information in the My Number Card and the realization of Sybil resistance based on the My Number Card while preserving anonymity even to the issuer. For the selective disclosure circuit, we also generated proof on an iOS device using mopro. Benchmarks for this proof generation are also included.

This is the end of the grant, but the MynaWallet development journey has only just begun. We will continue to develop for mass adoption and security of blockchain-based application and data sovereignty.

For those new to MynaWallet, we are developing the AA Wallet based on the My Number Card, a digital ID card issued by the Japanese government. So far, the MynaWallet team has been working on the following

  • Phase1
    • Realization of AA Wallet that can generate a tx using RSA digital signature key pair in My Number Card
  • Phase2
    • Verify the RSA digital signature of the x.509 certificate in the My Number Card and realize an AA Wallet generated from the public key of the RSA digital signature signed by the government

Overview

This time, we have realized the following two features by utilizing the My Number Card.

  • Selectively disclosure the information inside My Number Card and proof generation on iOS device
  • One of the ideas is to achieve sybil resistance while preserving the anonymity to the issuer
    • For example, this idea proposed by turboblitz is ideal for My Number Card.
    • The idea presented here is to provide sybil-resistance while preserving anonymity to the issuer, even if the root of sybil-resistance does not have a key pair for signature.
    • Also, we do not need to have assumptions that issuers of the key pair do not hold the list of secret keys.

Selectively disclose the information inside My Number Card

The digital ID card, My Number Card issued by the Japanese government, contains two certificates.

  • Electronic certificate for the bearer’s signature
    • This certificate is used when creating and sending electronic text via the Internet, etc.
    • It can be used to prove that “the electronic document created or transmitted is authentic and created by the user, and that the user sent it”.
  • Electronic certificate for user identification
    • Used when logging in to Internet sites, kiosk terminals at convenience stores, etc.
    • It can prove that “the person who logged in is the user himself/herself”.

The electronic certificate for the bearer’s signature contains the following four pieces of information about the user.

  • Name
  • Address
  • Gender
  • Age

The actual electronic certificate for the bearer’s signature is in x.509 format and is signed by the government using PKCS#1 v1.5 scheme including the above four information. To further utilize the identity provided by this number card, we have devised a scheme to verify the information using zkp and partially disclose this information to the blockchain. This scheme is designed to enhance interoperability with identities managed by other Identity Management Systems and applications that require the information in the My Number Card for authentication. Disclosing these personal information and placing them on-chain directly is kind of a digital tattoo, so what is actually disclosed is a Poseidon Hash with userSecret which is one of the parameters that users will decide by themselves. At this time, we decided to use Poseidon Hash which is friendly to zk-circuit, but it is still under discussion regarding the disclosure scheme since it is the commitment corresponding to the most important personal information.

Realization of Sybil Resistance and Anonymity to the government at the same time

Sybil Resistance is an important part currently missing in the crypto ecosystem. For example, Quadratic Funding proposed by Buterin, Hitzig, and Weil shows a way to allocate funds to public goods in a way that maximizes public utility. One of the reasons Quadratic Funding used to be a mere theoretical result is that its proof relies on an assumption that one person will not make multiple accounts on the voting system. Of course, this assumption does not hold in the real world… until now! We have completed a PoC implementation of a mechanism that prohibits a person from creating multiple Ethereum accounts, by utilizing a Japanese national ID card, based on the assumption that the Japanese government does not issue multiple cards for one person.

Organization

In this report, we first summarize the circuit details, benchmarks, and our considerations regarding the verification and selective disclosure of information in the My Number Card, followed by the circuit details, benchmarks, and our consideration regarding the realization of Sybil resistance while preserving privacy.

Selectively disclose the information inside My Number Card

Implementation

For implementation, the zk-email team has implemented

I’m using the following circuit implemented in snark-jwt-verify as a reference.

The following flow verifies the information in the my number card and discloses the information.

We think the following are some of the things we need to discuss.

  • Since the prover is responsible for entering an array for the mask, they can freely choose the byte sequence of the part of the x.509 certificate to be disclosed.
  • Since the part to be disclosed is fixed length, it can contain extra information at the back.

The first issue is solved by verifying the Object Identifier, which is a feature of x.509 certificates that indicates what information will follow. After masking, the part to be disclosed is brought to the head of the array in operation and the Object Identifier is verified, thereby restricting the free disclosure of information. As for the second issue, even if we can constrain the first part of the information to be disclosed in the My Number Card in the first issue, we cannot constrain the latter part of the information.

  • The length of the public part can never be longer than the reasonable length we determine for each information.
  • The byte sequence of the public part must be contiguous within the input byte sequence. Therefore, even if there is an extra byte sequence after the disclosed information, it is unlikely that the extra byte sequence will be a meaningful byte sequence and will not pass any verification afterwards based on this selectively disclosed information.

Benchmarks

This circuit was written in Circom and the proof protocol was Groth16 on BN254.

  • constraints: 1192222

Below are benchmarks of each Proof System on an M1 Macbook Air with 16GB RAM.

  • arkworks: 7.64 sec
  • rapidsnark: 23.5 sec
  • snarkjs (compiled to wasm): 42.4 sec

We also benchmarked on an actual iOS device using mopro.

  • iPhone12 Pro: 21.3 sec
  • iPhone15 Pro: 14.7 sec

Here is a video of it in action

demo video

Consideration

In addition to the circuits described above, the information in the My Number Card is encoded according to the DER format, which is expressed in the ASN.1 language. Therefore, we are also implementing the idea of reading the information on the My Number Card one by one according to this DER format.

Realization of Sybil Resistance and Anonymity to the issuer at the same time

Implementation

One of the unique ethos the crypto ecosystem cherishes is anonymity. We wanted to make sure that the Japanese government cannot tell which Ethereum account is tied to which MyNumber card. For this purpose we used a combination of merkle tree and zero knowledge proof, in a way similar to Tornado Cash.

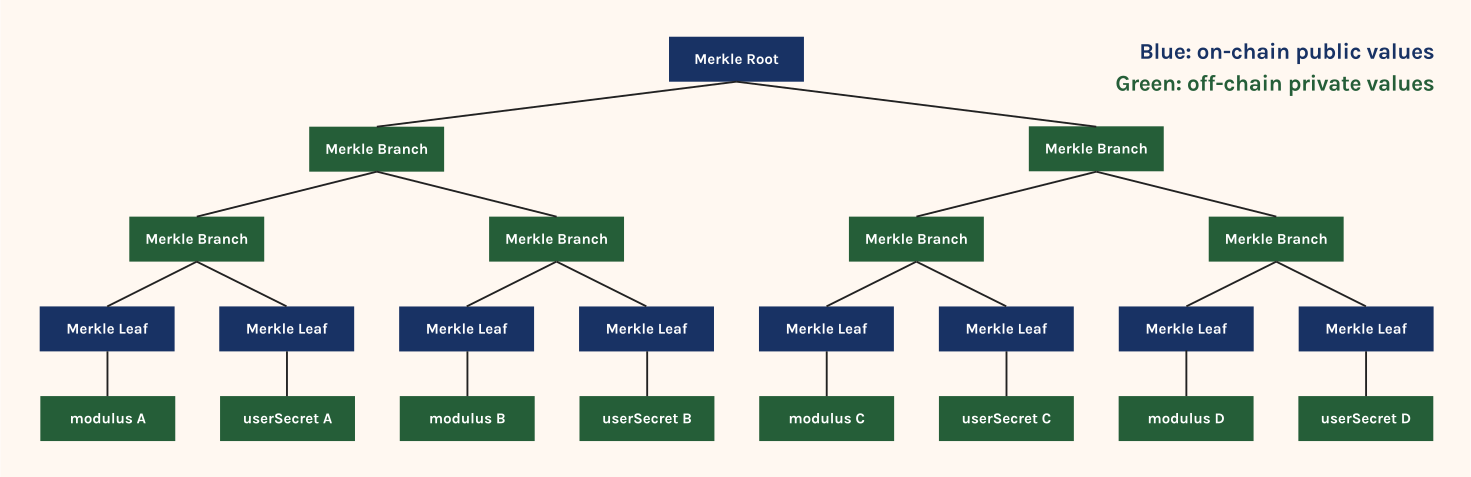
Figure 1. Conceptual diagram for this sybil resistance scheme

To activate a sybil resistant account, you add your public key (modulus N in the case of RSA signature) to merkle tree on-chain. In this process the smart contract will require you to submit a zkp that proves your public key is signed by the Japanese government. This ensures that every public key in the merkle tree is tied to a MyNumber card. We also commit to a nonce called userSecret in this process. The ethereum account address tied to MyNumber card is derived from CREATE2(Poseidon(publicKey + userSecret)). This address derivation process ensures that the government can’t derive an ethereum address from the public key, since the government does not know userSecret.

One problem with the scheme above is that the Japanese government may interact with the contract, and commit to userSecret unbeknownst to the user, since the government knows every citizen’s public key. To prevent this, the contract requires you to sign userSecret with the private key tied to the public key you wanna add to the merkle tree. Since the Japanese government does not know your private key (at least they claims so) This ensures that only a citizen can set his userSecret.

To use a sybil resistant ethereum account A, you will generate a zkp that says a) you know some merkle path b) the public key and the userSecret under that merkle path derives an ethereum account address A. If these properties are proven, our account abstraction wallet lets you issue transactions from that address. This scheme achieves both sybil resistance and anonymity, since this schemes ensures that

  • There is only one userSecret tied to a public key (modulus)
  • The public cannot tell which ethereum address is tied to which public key

The actual implementation can be found here

Benchmarks

We just mention the constraints number, since we believe that an detailed benchmarks on this circuit are not important compared to the structure of this scheme.

  • Circuit for registration to a Merkle Tree of depth 16
    • constraints: 179274
  • Verification circuits for a Merkle Tree of depth 16
    • constraints: 5817

Further Implementation

Also using the recent advancements in zero-knowledge lookup argument research, we might be able to throw away the use of merkle tree altogether. This is good because it reduces the time it takes to generate a proof.